Fräiheetsgrad
| Dësen Artikel ass eréischt just eng Skizz. Wann Dir méi iwwer dëst Theema wësst, sidd Dir häerzlech invitéiert, aus dëse puer Sätz e richtegen Artikel ze schreiwen. Wann Dir beim Schreiwen Hëllef braucht, da luusst bis an d'FAQ eran. |
Mat Fräiheetsgrad gëtt d'Zuel vun de fräi wielbaren, vuneneen onofhängege Beweegungsméiglechkeete vun engem System bezeechent. En onbeweegleche Kierper am Raum huet deemno de Fräiheetsgrad , well et kann een de Kierper an dräi vuneneen onofhängege Richtunge beweegen an an dräi vuneneen onofhängege Plangen dréien. An dëser Bedeitung als Ganzzuel vun den onofhängege Beweegungsméiglechkeete kënnt de Begrëff Fräiheetsgrad nëmmen am Singular vir.[1] Déi eenzel Beweegungsméiglechkeete ginn dann och Fräiheete genannt. An der Literatur an am allgemenge Sproochgebrauch gëtt awer och jiddwereng vun den onofhängege Beweegungsméiglechkeete vun engem System als e Fräiheetsgrad bezeechent.[2] En onbeweegleche Kierper ouni Uschloss huet sechs Fräiheetsgraden.
Mechanik[änneren | Quelltext änneren]
All Fräiheetsgrad vun engem physikalesche System entsprécht enger onofhängeger (verallgemengerter Koordinat), mat där d'System beschriwwe ka ginn. Wat mat dem Wuert "onofhängeg" gemengt ass, gesäit een un engem Beispill: Ugeholl en Deelche ka sech nëmme laanscht eng riicht Linn um Plang (z. B. op engem Dësch) beweegen,. Wann een als onofhängeg Koordinaten de Wee op der Linn unhëlt da kënnen d'x-Koordinaten an d'y-Koordinate berechent ginn.
D'Zuel vun de verallgemengerte Koordinaten ass eng Systemeegeschaft. Beispillsweis huet e fräie Massepunkt dräi Translatiounsfräiheetsgraden. En onbeweegleche Kierper dogéint huet nieft den dräi Translatiouns- nach dräi Rotatiounsfräiheetsgraden, déi lescht ginn duerch säin Dréiwénkel beschriwwen.
Gelenker[änneren | Quelltext änneren]
Um Gelenk vun engem Mechanissem sinn zwéin Deeler mateneen beweeglech verbonnen. De Fräiheetsgrad ass d'Zuel vun de méigleche Beweegungen, déi d'Gelenk ausféiere kann. Dobäi stinn d'Fräiheete vum onbeweegleche Kierper zur Dispositioun. Bannen an engem Gelenk gëtt op d'mannst eng Fräiheet ënnerbonnen, maximal fënnef Fräiheeten sti fir en technesche Gebrauch zur Dispositioun. Méi wéi dräi Fräiheete gi mat Méifachgelenker erreecht.
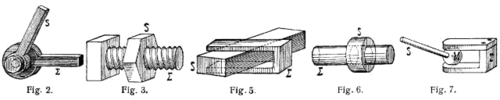
- Figur 2: Dréigelenk
- Figur 3: Schraufgelenk
- Figur 5: Dréischubgelenk, Plackegelenk
- Figur 6: Dréischubgelenk
- Figur 7: Kugelgelenk
D'Zuel vun de Fräiheete vun engem System, dat aus villen Deelsystemer geformt gëtt, ass d'Zomm vu Fräiheete vun den Deelsystemer, sou wäit dës net duerch Zwangsbedéngunge (z. B. Gefierkupplung: Den Unhänger ka sech net onofhängeg vum Zuchgefier beweegen) ageschränkt gëtt.
- e Fräiheesgrad >0 beschreift een a sech beweeglecht System (Mechanissem).
- e Fräiheetsgrad =0 beschreift e statesch bestëmmten System.
- e Fräiheetsgrad <0 steet fir e statesch iwwerbestëmmte System, an deem staark bannenzeg Spannungen optriede kënnen („klemmt“).
Thermodynamik[änneren | Quelltext änneren]
D'Zuel vun de Fräiheeitsgrade vun engem System spillt och an der Thermodynamik eng Roll, well sech d'Energie gläichméisseg op déi eenzel Fräiheetsgrade verdeelt. D'Zuel vun de Fräiheetsgrade geet dofir och an d'Entropie an, déi jo zum Schluss eng Mooss fir d'Zuel vun den erreechbaren Zoustänm ass. Thermodynamesch Systemer hu generell ganz vill Fräiheetsgrade, ongeféier an der Gréisst vun 1023. Et kënnen allerdéngs vill gläichaarteg Systemer mat jee nëmme wéinege Fräiheetsgraden zousta kommen, zum Beispill 1023 Atomer mat effektiv (kuckt ënnen, jee dräi Fräiheetsgraden).
Et kann een déi bannenzeg Energie vun engem ideale Gas an Ofhängegkeet vun der Temperatur an der Zuel vun de Fräiheetsgrade vun engem Gasdeelchen uginn. Am Normalfall vun engem eenatomegen ideale Gas mat Deelchen ergëtt sech mat der Boltzmann-Konstant
- .
Allgemeng gëllt:
- .
Heibäi ass wichteg, datt zu der Bestëmmung vun bannenzeg Fräiheitsgrade duebel gezielt ginn, well d'Schwingunge souwuel kinetesch wéi och potentiell Energie hunn (kuckt ënnen).
Opgrond vun den diskreeten Energieniveaue vun der Quantemechanik kënne bei niddregen Energië meeschten net all Fräiheetsgrade ugereegt ginn, well den éischten ugereegten Zoustand schonn eng ze héich Energie huet. Doduerch kann e System bei enger gegiewener Energie effektiv manner Freiheitsgraden hunn. Zum Beispiel huet en Atom bei Raumtemperatur effektiv nëmmen déi dräi Translatiounsfräiheetsgraden, well déi mëttel Energie sou niddreg ass, datt et praktesch keng Ureegunge gëtt.
En zweeatomegt Moleküll wéi molekulare Waasserstoff huet – nieft den elektroneschen Ureegungen – sechs Fräiheetsgrade: Dräi vun der Translatioun, zwéi vun der Rotatioun, an e Schwéngungsfräiheetsgrad (deen allerdéngs bei der Berechnung vun der bannenzeger Energie duebelt zielt). Rotatioun a Schwéngung sinn quantiséiert a bei klenger Gesamtenergie vun engem Moleküll kënnen energeetesch méi héich leiende Rotatiouns- a Schwéngungsfräiheetsgrade net ugereegt ginn; e seet ee si wieren "agefruer." Sou verhale sech déi meescht zweeatomeg Gase wéi zum Beispill Waasserstoff, Sauerstoff oder Stéckstoff ënner Normalbedéngungen effektiv sou, als hätten d'Eenzelmolekülle nëmme fënnef Fräiheetsgrade, wat sech am Adiabatenexponenten ofliese léisst. Bei héijen Temperature sinn dem System all Fräiheetsgrade zougänglech.

Méi komplex Molekülle hu méi Schwéngungsfräiheetsgrade, a liwwere sou méi e grousse Bäitrag zu der Entropie.
Jiddwer Moleküll mat Atomer huet Fräiheetsgraden, well ee fir jiddwer Atom dräi Koordinate brauch fir seng Positioun ze definéieren. Déi kann ee formal an Translatiouns-, Rotatiouns- a bannenzeg Schwéngungsfräiheetsgraden andeelen.
Heibäi gëllt
- fir -atomeg linear Moleküllen:
- Translatiounsfräiheetsgraden,
- Rotatiounsfräiheetsgraden,
- Schwéngungsfräiheetsgraden (déi bei der Berechnung vun der bannenzeger Energie duebel zielen),
- fir -atomeg net linear Moleküllen:
- Translatiounsfräiheetsgraden,
- Rotatiounsfräiheetsgraden,
- Schwéngungsfräiheetsgraden (déi bei der Berechnung vun der bannenzeger Energie duebel zielen).
E Moleküll mat Atomer huet fir déi bannenzeg Schwéngungsenergie allgemeng
Schwéngungsfräiheetsgrade.
| Stoff | Fräiheitsgrade | |||
|---|---|---|---|---|
| Translatioun | Rotatioun | Schwéngung (duebel ze zielen) | Zomm | |
| Gasmoleküll, 1-atomeg | +3 | +0 | 2×(3×1−3−0)=+0 | 3 |
| Gasmoleküll, 2-atomeg | +3 | +2 | 2×(3×2−3−2)=+2 | 7 |
| Gasmoleküll, 3-atomeg linear | +3 | +2 | 2×(3×3−3−2)=+8 | 13 |
| Gasmoleküll, 3-atomeg gewénkelt | +3 | +3 | 2×(3×3−3−3)=+6 | 12 |
| 1 Atom am Festkierper | +0 | +0 | 2×(3×1−0−0)=+6 | 6 |
Déi thermodynamesch Fräiheetsgrade vun der Zoustandgréissten op makroskopeschem Niveau erginn sech fir Systemer am Gläichgewiicht iwwer d'Gibbssche Phasereegel.
Kuckt ouch[änneren | Quelltext änneren]
Um Spaweck[änneren | Quelltext änneren]
Referenzen[Quelltext änneren]
- ↑ Wolfgang H. Müller, Ferdinand Ferber: Technische Mechanik für Ingenieure: Geeignet für die Bachelor-ausbildung
- ↑ Eberhard Brommundt, Gottfried Sachs, Delf Sachau: Technische Mechanik: Eine Einführung


















