Penrose-Dräieck

Dësen Artikel ass eréischt just eng Skizz. Wann Dir méi iwwer dëst Theema wësst, sidd Dir häerzlech invitéiert, aus dëse puer Sätz e richtegen Artikel ze schreiwen. Wann Dir beim Schreiwen Hëllef braucht, da luusst bis an d'FAQ eran.

De Penrose-Dräieck

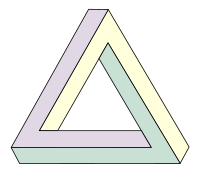
De Penrose-Dräieck, och Tribar genannt, ass déi bekanntst vun den onméigleche Figuren. Se weist dräi Dunnen, déi alleguer am rechte Wénkel matenee verbonne sinn, an anengems en Dräieck duerstellen. Op déi Manéier verstéisst déi Figur géint e puer Gesetzer vun der Euklidescher Geometrie, ënner anerem muss d'Zomm vun de Wénkelen an engem Dräieck ëmmer 180° sinn.

Bildung vum Penrose-Dräieck aus partielle Figuren

Bildung vum Penrose-Dräieck (riets) aus zwou Partialfiguren

Wann de lénksen Deel vun der Figur parallel zur rietser Säit beweegt gëtt, bis säin ieweschten horizontale Rand mat dem ieweschten horizontale Rand vum mëttleren Deel zesummefält, entsteet de Penrose-Dräieck (riets) duerch d'Iwwerlappung vun den zwéin Deeler. Déi éischt zwou deelweis Vuë vum Penrose-Dräieck sinn eenzel erkennbar, wärend den Dräieck, deen doraus entsteet, eng onméiglech Figur representéiert.

Geschicht vum Penrose-Dräieck

Fir d'éischt Kéier gouf de Penrose-Dräieck 1934 vum schweedesche Kënschtler Oscar Reutersvärd gezeechent.

Um Spaweck

Commons: Penrose-Dräiecker – Biller, Videoen oder Audiodateien