Warscheinlechkeet

D' Warscheinlechkeet oder Probabilitéit ass eng Astufung vun Aussoen an Urteeler nom Grad vun der Gewëssheet (Sécherheet). Besonnesch Bedeitung huet dobäi d'Gewëssheet vu Viraussoen. An der Mathematik huet sech mat der Warscheinlechkeetstheorie en eegent Fachgebitt entwéckelt, dat d'Warscheinlechkeeten als mathematesch Objete beschreift, deenen hir formal Eegenschaften am Alldag an an der Philosophie och op Aussoen an Urteeler iwwerdroe ginn.

Warscheinlechkeetsopfaassungen

Et gëtt ënnerschiddlech Opfaassunge vu Warscheinlechkeeten (Warscheinlechkeetsbegrëffer).

Symmetrieprinzip – klassesch oder laplacesch Opfaassung

D'Warscheinlechkeet vun engem Evenement ass d'Verhältnes vun de gënschtege Resultater zum ganzen Iwwermooss vun de Resultater. Sou ass zum Beispill d'Warscheinlechkeet, mat engem Wierfel eng ongerued Zuel ze werfen, 0,5. Dat entsprécht enger relativer Heefegkeet vu 50 %, well et gëtt sechs méiglech Resultater, vun deenen der dräi déi genannt Eegenschaft hunn.

Dat ass déi sougenannt klassesch Definitioun, wéi se vum Christiaan Huygens an vum Jakob I. Bernoulli entwéckelt a vum Laplace formuléiert gouf. Si ass d'Grondlag vun der klassescher Warscheinlechkeetstheorie. D'Elementarevement huet gläichwäerteg Antrëttswarscheinlechkeeten. Viraussetzung ass en endlech Resulatraum an d'Kenntnes vun den A-priori-Warscheinlechkeeten.

Beispill: Bei engem faire Wierfel (dat heescht kee Resultat gëtt duerch onsymmetresch Masseverdeelung oder Änleches avantagéiert) iwwerleet ee sech, datt all Zuel déi selwecht Chance huet an dofir an 1/6 vun alle Versich erschéngt. D'Warscheinlechkeet vum Evenement „gerued Zuel“ berechent een sou: Et gëtt dräi gënschteg Resultater (2, 4, 6), awer sechs méiglech Resultater, dofir kritt een 3/6 = 0,5 als Resultat.

Objetivistesche Warscheinlechkeetsbegrëff

Haaptartikel zu dësem Theema: Objetivistesche Warscheinlechkeetsbegrëff

Heefegkeetsprinzip – Statistesch Warscheinlechkeetsopfaassung

En Zoufallsexperiment gëtt sou dacks wéi méiglech widderholl, da ginn d'relativ Heefegkeete vun de jeeweilegen Elementarevenementer berechent. D'Warscheinlechkeet vun engem Evenement ass elo de Grenzwäert vu senger relativer Heefegkeet bei (theoreetesch) onendlech ville Widderhuelungen. Dat ass déi sougenannt ‚Limes-Definitioun‘ nom von Mises. D'Gesetz vun de groussen Zuelen spillt hei eng zentral Roll. Viraussetzung ass déi belibeg Widderhuelbarkeet vum Experiment; déi eenzel Duerchgäng musse vuneneen onofhängeg sinn. En aneren Numm fir dat Konzept ass Frequentistesche Warscheinlechkeetsbegrëff. Dëse Warscheinlechkeetsbegrëff ass zum Beispill an der Physik bei der Zerfallswarscheinlechkeet vun engem Radionuklid gemengt; d'Experimenter sinn hei déi eenzel, vuneneen onofhängeg Atomkärenzerfäll.

Beispill: Et wierfelt een 1000-mol a kritt follgend Verdeelung: D'Zuel 1 fält 100-mol (dat ass eng relativ Heefegkeet vun 10 %), d'Zuel 2 fält 150-mol (15 %), d'Dräi och 150-mol (15 %), d'Véier 20 %, d'Fënnef 30 % an d'Sechs 10 % vun alle Fäll. De Verdacht kënnt op, datt de Wierfel net fair ass. No 10.000 Duerchgäng hu sech d'Zuele bei den ugewisene Wäerter stabiliséiert, soudatt ee mat zimmlecher Sécherheet soe kann, datt zum Beispill d'Warscheinlechkeet, eng 3 ze wierfelen, bei 15 % läit.

Propensitéitstheorie

D'Propensitéitstheorie interpretéiert Warscheinlechkeet als Mooss fir d'Tendenz vun engem Prozess zu engem bestëmmte Resultat.

Quantemechanesch Warscheinlechkeetsopfaassung

An der netrelativistescher Quantemechanik gëtt d'Wellefunktioun vun engem Deelchen als seng fundamental Beschreiwung gebraucht. Den Integral vum Mengequadrat vun der Wellefunktioun iwwer e Raumgebitt entsprécht do der Warscheinlechkeet, d'Deelchen doran ze fannen. Et handelt sech also net ëm eng statistesch, mä ëm eng net-determinéiert Warscheinlechkeet.

Subjektivistesch Warscheinlechkeetsopfaassung

Haaptartikel zu dësem Theema: Subjektivistesch Warscheinlechkeetsopfaassung

Bei eemolegen Zoufallsevenementer kann een d'Antrëttswarscheinlechkeet nëmme schätzen. Zentral Gesiichtspunkte sinn hei Expertwëssen, Erfarung an Intuitioun. Dofir schwätzt ee vun enger subjektivistescher Warscheinlechkeetsopfaassung, kuckt och Bayessche Warscheinlechkeetsbegrëff.

Beispill: Nodeem ee verschidden Autoen hat, schätzt hien d'Warscheinlechkeet als héich an (zum Beispill „Ech si mir zu 80 % sécher“), mat der Mark XY och beim nächsten Autokaf nees zefridden ze sinn. Dëse Viraussowäert kann zum Beispill duerch en Testbericht no uewen oder ënne verännert ginn.

Axiomatesch Definitioun vun der Warscheinlechkeet

Axiomatesch Definitioun vun der Warscheinlechkeet no Kolmogorow – déi haut fir d'Mathematik moosgiewent Definitioun, kuckt Axiome vun Kolmogorow.

Stochastik

Haaptartikel zu dësem Theema: Stochastik

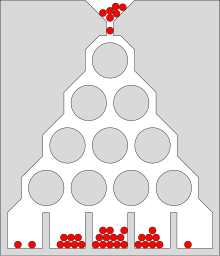
Stochastik als en Deelgebitt vun der Mathematik ass d'Léier vun der Heefegkeet an der Warscheinlechkeet. Si ass e verhältnesméisseg jonken Deelberäich vun der Mathematik, zu deem am weidere Sënn och d'Kombinatorik, d'Warscheinlechkeetstheorie an d'mathematesch Statistik gehéieren.

Heefeg gëtt de mathematesche Begrëff vun der Warscheinlechkeet gebraucht: d'Warscheinlechkeetsrechnung oder d'Warscheinlechkeetstheorie (Deelgebitt vun der Stochastik) këmmert sech ëm déi mathematesch Systematiséierung vu Warscheinlechkeeten. Hei ginn Warscheinlechkeetsverdeelung, Warscheinlechkeetsfunktioun, bedingt Warscheinlechkeet a vill aner Begrëffer ënnerscheet.

Warscheinlechkeeten sinn Zuelen tëscht 0 an 1, woubäi Null an Eent zoulässeg Wäerter sinn. Engem onméiglechen Evenement gëtt d'Warscheinlechkeet 0 zougewisen, engem sécheren Evenement d'Warscheinlechkeet 1. D'Ëmkéierung dovu gëllt awer nëmme wann d'Zuel vun allen Evenementer héchstens ofzielbar onendlech ass. An „iwwerofzielbar onendlechen“ Warscheinlechkeetsraim kann en Evenement mat Warscheinlechkeet 0 antrieden, et heescht dann bal onméiglech, en Evenement mat Warscheinlechkeet 1 muss net antrieden, et heescht dann bal sécher.

Psychologie – Aschätze vu Warscheinlechkeeten

Et gëtt dacks behaapt, de Mënsch hätt e schlecht Gefill fir d'Warscheinlechkeet, et schwätzt een an deem Fall och vum „Warscheinlechkeetsidiot“. Dozou follgend Beispiller:

De Gebuertsdagsparadoxon: Op engem Foussballterrain sinn 23 Persounen (zweemol eelef Spiller an ee Schidsriichter). d'Warscheinlechkeet, datt dorënner op d'mannst zwou Persounen de selwechten Dag Gebuertsdag hunn, ass méi grouss wéi 50 %.
Dir hutt e medezineschen Checkup gemaach an e positiivt Resultat kritt. Dir wësst zousätzlech, datt Dir am Verglach zu der ganzer Bevëlkerung keng besonnesch Risikofaktore fir déi diagnostizéiert Krankheet hutt: Mat de Rechemethode vun der bedéngter Warscheinlechkeet kann een den tatsächleche Risiko ofschätzen, datt déi duerch den Test verfaasst Diagnos tatsächlech zoutrëfft. Dobäi sinn zwou Donnéeë vu besonnescher Bedeitung, fir de Risiko vun engem falsch positive Resultat ze ermëttelen: d'Zouverlässegkeet (Selektivitéit an Spezifitéit) vum Test an déi observéiert Grondheefegkeet vun der betreffender Krankheet an der ganzer Ëffentlechkeet. Dësen tatsächleche Risiko ze kennen kann dobäi hëllefen, de Sënn vu weideren (ënner Ëmstänn follgeräiche) Behandlungen ofzeweien. A sou Fäll ergëtt d'Duerstellung vun der absolutter Heefegkeet um vollstännegen Entscheedungsbam an een dorop opbauend Berodungsgespréich mat dem Dokter e besseren Androck wéi déi blouss Interpretatioun vu Prozentzuelen duerch isoléiert Testresultater.

Philosophie – Verständnes vu Warscheinlechkeet

Wärend iwwer de mathemateschen Ëmgank mat Warscheinlechkeeten wäitgoend Eenegkeet besteet (kuckt Warscheinlechkeetstheorie), ass awer Oneenegkeet doriwwer, wourop d'Rechenreegelen vun der mathematescher Theorie benotzt soll ginn. Dat féiert zu der Fro no der Interpretatioun vum Begrëff „Warscheinlechkeet“.

Heefeg gëtt „Warscheinlechkeet“ bei zwéi verschiddenen Zesummenhäng gebraucht:

Aleatoresch Warscheinlechkeet (och: ontesch/objektiv/statistesch Warscheinlechkeet) beschreift déi relativ Heefegkeet vun Evenementer, déi vun engem zoufällege physikalesche Prozess bestëmmt ginn. Méi genee ënnerscheet een deterministesch physikalesch Prozesser, déi mat genuch geneeër Informatioun am Prinzip viraus ze soe wieren (Wierfelworf, Wiederprognos), an netdeterministesch Prozesser, déi prinzipiell net virauszesoe sinn (radioaktiven Zerfall).
Epistemesch Warscheinlechkeet (och: subjektiv/personell Warscheinlechkeet) beschreift d'Onsécherheet iwwer Aussoen, bei deene kausal Zesummenhäng an Hannergrënn nëmmen onvollstänneg bekannt sinn. Déi Aussoe kënne sech op vergaangen oder zukünfteg Evenementer bezéien. Naturgesetzer ginn zum Beispill geleeëntlech epistemesche Warscheinlechkeeten zougeuerdent, wéi och Aussoen a Politik („D'Steiersenkung kënnt mat 60 % Warscheinlechkeet.“), Wirtschaft oder Rechtsspriechung.

Aleatoresch an epistemesch Warscheinlechkeet si labber mat dem frequentisteschen an dem bayesschen Warscheinlechkeetsbegrëff associéiert.

Et ass eng oppe Fro, ob sech aleatoresch Warscheinlechkeet op epistemesch Warscheinlechkeet reduzéiere léisst (oder ëmgekéiert): Erschéngt eis d'Welt zoufälleg, well mir net genuch iwwer si wëssen, oder gëtt et fundamental zoufälleg Prozesser, wéi z. B. d'objektiv Deitung vun der Quantemechanik unhëlt? Obwuel fir béid Standplazen déi selwecht mathematesch Reegelen zum Ëmgank mat Warscheinlechkeeten zielen, huet déi jeeweileg Siichtweis wichteg Konsequenzen dofir, déi mathematesch Modeller als gëlteg ugesi ginn.

Kuckt och

Literatur

Jacob Rosenthal: Wahrscheinlichkeiten als Tendenzen. Eine Untersuchung objektiver Wahrscheinlichkeitsbegriffe. Mentis, Paderborn 2004. ISBN 3-89785-373-6 (Guter Überblick über die philosophischen Deutungen der Wahrscheinlichkeit, vor allem über die aleatorischen respektiv ontischen Deutungen)
Vic Barnett: Comparative Statistical Inference. John Willey & Sons, Chichester 1999. ISBN 978-0471976431

Um Spaweck